Project Website - Edge Grasp Network - A Graph-Based SE(3)-invariant Approach to Grasp Detection
Abstract: Given point cloud input, the problem of 6-DoF grasp pose detection is to identify a set of hand poses in $\mathrm{SE}(3)$ from which an object can be successfully grasped. This important problem has many practical applications. Here we propose a novel method and neural network model that enables better grasp success rates relative to what is available in the literature. The method takes standard point cloud data as input and works well with single-view point clouds observed from arbitrary viewing directions.
Short Video Introduction
Paper PDF • CODE • Poster • Video • ICRA 2023
Khoury College of Computer Science, Northeastern University
Introduction
In the following parts, we first describe what is and why edge grasp. Then, introduce our representation of edge grasp step by step. After that, we explore and realize the $\mathrm{SE}(3)$ symmetry inside our representation to get better performance. The simulated experiment part of our paper is based on the simulator of VGN, a simulation environment in PyBullet for 3D grasping. Finally, we implement our method on the real robot and test four different object sets. Check our paper for more details.
Motivation and description
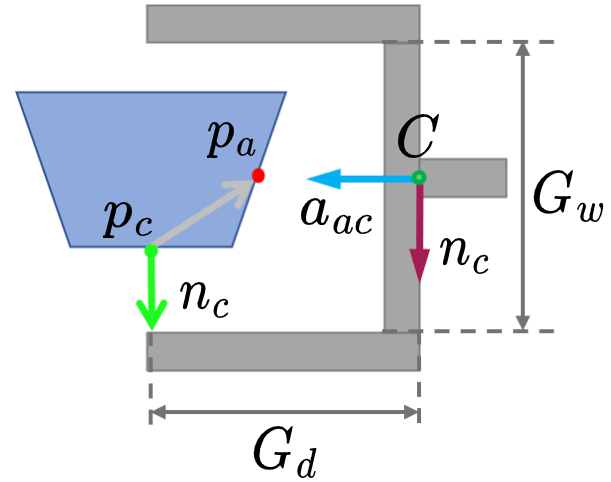
Detecting 6-DoF antipodal grasping pose in the point cloud captured by a single camera view is not an easy taks due to the occulusion. We still have some useful information to construct a clear grasp pose, e.g., the gripper must contact on one point; the surface normal direction of the contact point could support enough friction; parallel-jaw gripper is symmetric. Based on the clues, our 6-DoF edge grasp is clearly defined with an approach point $p_a$ and a contact point $p_c$. Assuming that we can estimate the object surface normal $n_c$ at point $p_c$, $(p_a, p_c)$ defines a grasp orientation $R$ where the gripper fingers move parallel to the vector $n_c$ and the gripper approaches the object along the vector $a_{ac} = n_c \times (n_c \times (p_a - p_c))$. The gripper center $C$ is positioned such that $p_a$ is directly between the fingers and $p_c$ is at a desired point of contact on the finger, $C = p_a - \delta a_{ac}$. Here, $\delta = G_d + (p_a-p_c)^T a_{ac}$ denotes the distance between the center of the gripper and $p_a$ and $G_d$ denotes gripper depth.
One key advantage of this sampling method is that we can easily provide the approximate position of a desired grasp as an input to the model. If we want to grasp a tool by its handle, for example, this is easily achieved by only considering approach positions and contact locations on the handle.
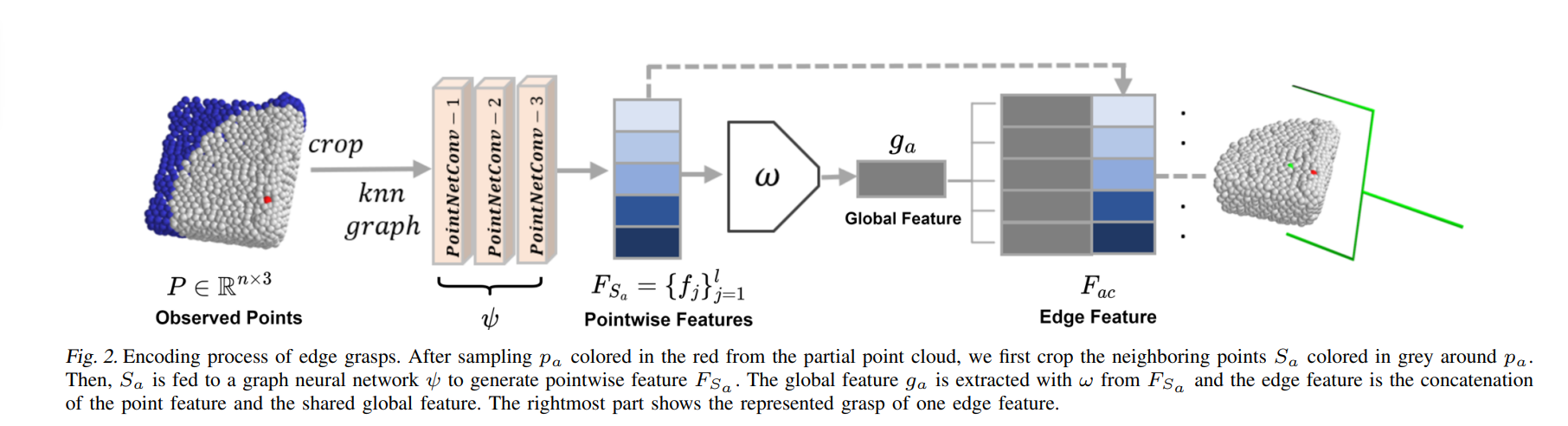
Representation and $\mathrm{SE}(3)$ invariance
It is natural to consider using edge that connects the approch point and the contact point to represent such grasp. Specically, we use a graph neural network to generate the local feature of the contatc point and the global feature of the approach point to build our edge feature. The detailed encoding process is shown in the figure above. Let’s define $P$ as the observed point cloud and $\alpha$ as the 6-DoF grasp. The grasp evaluation problem is to find a function $\Phi: (P, \alpha) \mapsto [0,1]$, that denotes the quality of grasp $\alpha$. Notice that $\Phi$ is invariant to translation and rotation in the sense that $\Phi(g \cdot P, g \cdot \alpha) = \Phi(P,\alpha)$ for an arbitrary $g \in \mathrm{SE}(3)$. In other words, the predicted quality of a grasp attempt should be invariant to transformation of the object to be grasped and the grasp pose by the same rotation and translation. The translation invariance could be achieved by trasnlating the point cloud. We enable rotational invariance with two different approaches. The first approach is to use data augmentation and the second approach is to use an $\mathrm{SO}(3)$-equivariant model, Vector Neurons. As we show in our paper, leveraging $\mathrm{SO}(3)$ symmetries is beneficial to learn a grasp function.
Real Robot Experiment
We measure physical grasp performance with 4 different object sets. As shown in the figure below, the first row shows the object sets and the second row shows the configurations. From the left column to the right column, there are packed scenarios from 10 objects, pile scenarios from 10 objects, 20 test hard objects, and 12 berkeley adversarial objects.

10 packed objects

10 pile objects

20 test hard objects

12 Berkeley adversarial objects
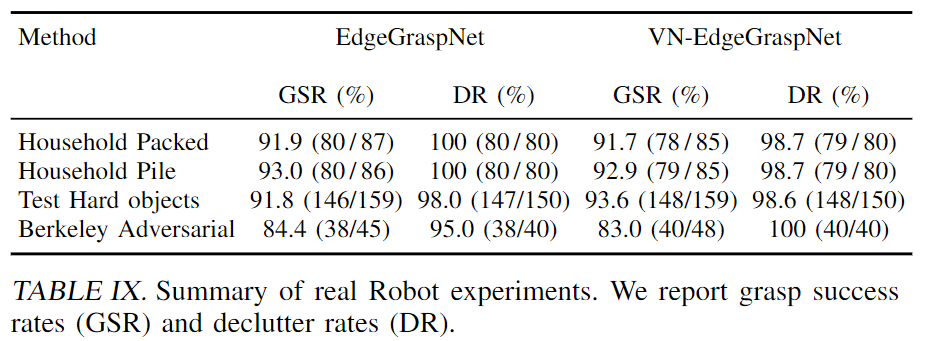
The table above shows the grasp success rate (GSR that measures the ratio of successful grasps to total grasps) and declutter rate (DR that measures the ratio of objects removed successfully to the number of total objects presented) of the real robot experiments.
Adversarial Objects-Edge Grasp Net-5 Runs
Test-Hard Objects-VN-Edge Grasp Net-15 Runs
Real-Time Grasp Detection
Real-World Grasp Experiments-Video Summary
Citation
@article{huang2022edge,
title={Edge Grasp Network: A Graph-Based SE (3)-invariant Approach to Grasp Detection},
author={Huang, Haojie and Wang, Dian and Zhu, Xupeng and Walters, Robin and Platt, Robert},
journal={arXiv preprint arXiv:2211.00191},
year={2022}
}
Contact
huang dot haoj @ northeastern dot edu




