Project Website - Equivariant Transporter Network

Abstract:

Many challenging robotic manipulation problems can be viewed through the lens of a sequence of pick and pick-conditioned place actions. Recently, Transporter Net proposed a framework for pick and place that is able to learn good manipulation policies from a very few expert demonstrations. A key reason why Transporter Net is so sample efficient is that the model incorporates rotational equivariance into the pick-conditioned place module, i.e., the model immediately generalizes learned pick-place knowledge to objects presented in different pick orientations. This work proposes a novel version of Transporter Net that is equivariant to both pick and place orientation. As a result, our model immediately generalizes pick-place knowledge to different place orientations in addition to generalizing pick orientation as before. Ultimately, our new model is more sample efficient and achieves better pick and place success rates than the baseline Transporter Net model. Our experiments show that only with 10 expert demonstrations, Equivariant Transporter Net can achieve greater than 95% success rate on 7/10 tasks of unseen configurations of Ravens-10 Benchmark. Finally, we augment our model with the ability to grasp using a parallel-jaw gripper rather than just a suction cup and demonstrate it on both simulation tasks and a real robot.

Paper PDF • CODE • RSS 2022

Khoury College of Computer Science, Northeastern University

Elevator Pitch

Equivariance in Pick and Place

Pick and place is an important topic in manipulation due to its value in industry. Traditional assembly methods in factories require customized workstations so that fixed pick and place actions can be manually predefined. Recently, considerable research has focused on end-to-end visioned based models that directly map input observations to actions, which can learn quickly and generalize well. However, due to the large action space, these methods often require copious amounts of data.

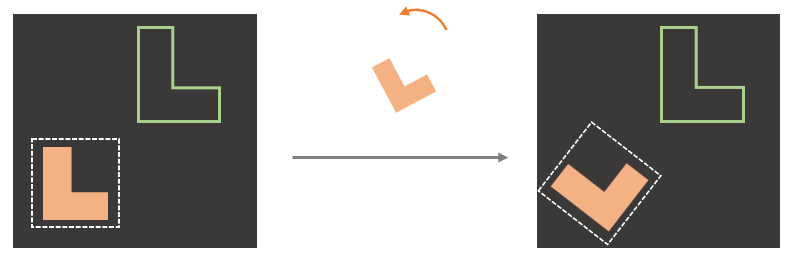
$C_n$ Equivariance

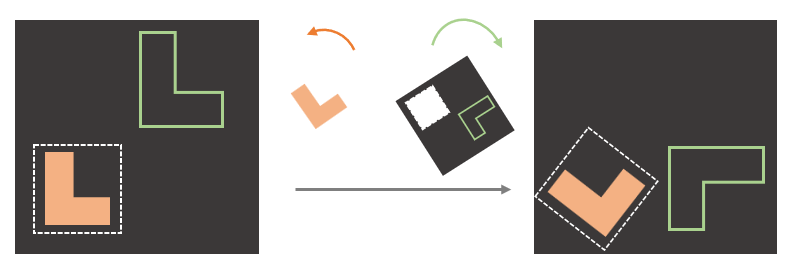
$C_n \times C_n$ Equivariance

A recent sample-efficient framework, Transporter Net, detects the pick-conditioned place pose by performing the cross convolution between an encoding of the scene and an encoding of a stack of differently rotated image patches around the pick. As a result of this design, Transporter Net is equivariant with respect to pick orientation. As shown in the left figure above, if the model can correctly pick the pink object and place it inside the green outline when the object is presented in one orientation, it is automatically able to pick and place the same object when it is presented in a different orientation. This symmetry over object orientation enables Transporter Net to generalize well and it is fundamentally linked to the sample efficiency of the model. Assuming that pick orientation is discretized into n possible gripper rotations, we will refer to this as a $C_n$ pick symmetry, where $C_n$ is the finite cyclic subgroup of $SO(2)$ that denotes a set of $n$ rotations.

Although Transporter Net is $C_n$-equivariant with regard to pick, the model does not have a similar equivariance with regard to place. That is, if the model learns how to place an object in one orientation, that knowledge does not generalize immediately to different place orientations. This work seeks to add this type of equivariance to the Transporter Network model by incorporating $C_n$-equivariant convolutional layers into both the pick and place models. Our resulting model is equivariant both to changes in pick object orientation and changes in place orientation. This symmetry is illustrated in right figure and can be viewed as a direct product of two cyclic groups, $C_n \times C_n$. Enforcing equivariance with respect to an even larger symmetry group than Transporter Net leads to even greater sample efficiency since equivariant neural networks learn effectively on a lower dimensional action space, the equivalence classes of samples under the group action. Thus a larger group results in an even smaller dimensional sample space and thus better coverage by the training data.

Highlight

In our paper, we will first go through the design of Transporter Net and prove its $C_n$ Equivariance theoretically. Then, extend it to $C_n \times C_n$ Equivariance smoothly. The key point inside $C_n \times C_n$ Equivariance is the Relativity Property, i.e., a rotation on the picked object is equivariant to an inverse rotation on the placement. The entire proofs are shown step by step in our Appendix.

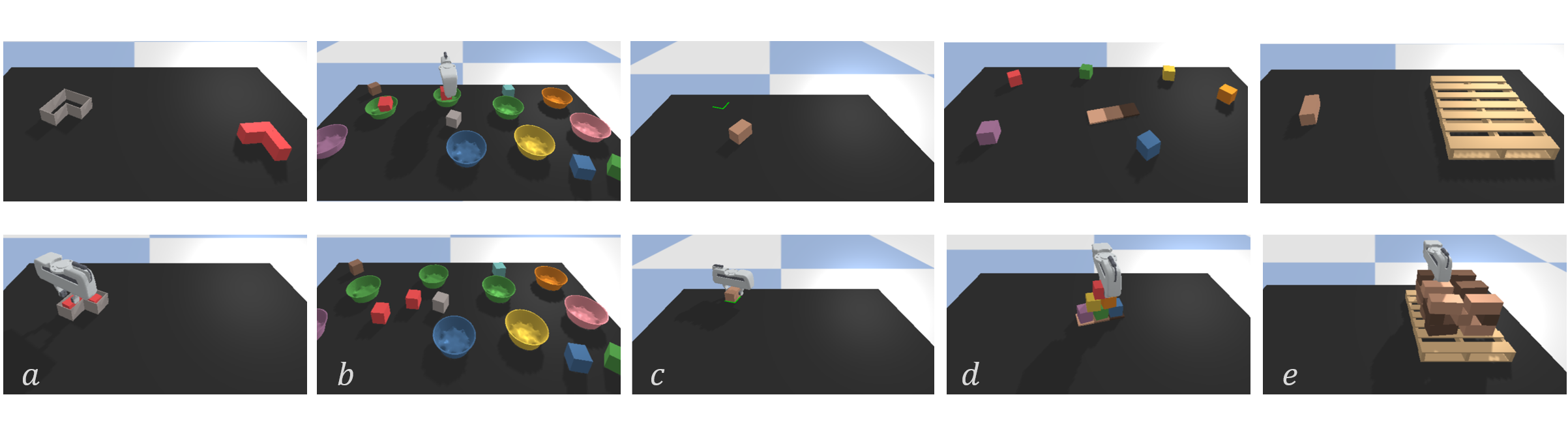
The experiment part of our paper is based on Ravens, a simulation environment in PyBullet for 2D robotic manipulation with emphasis on pick and place. Since Ravens uses suction gripper that doesn’t require pick angle inference, we select five tasks shown below and provide a Panda-Gripper version simulated Environment. It inherits the Gym-like API from Ravens, each with (i) a scripted oracle that provides expert demonstrations and (ii) reward functions that provide partial credit. Check our code for more details.

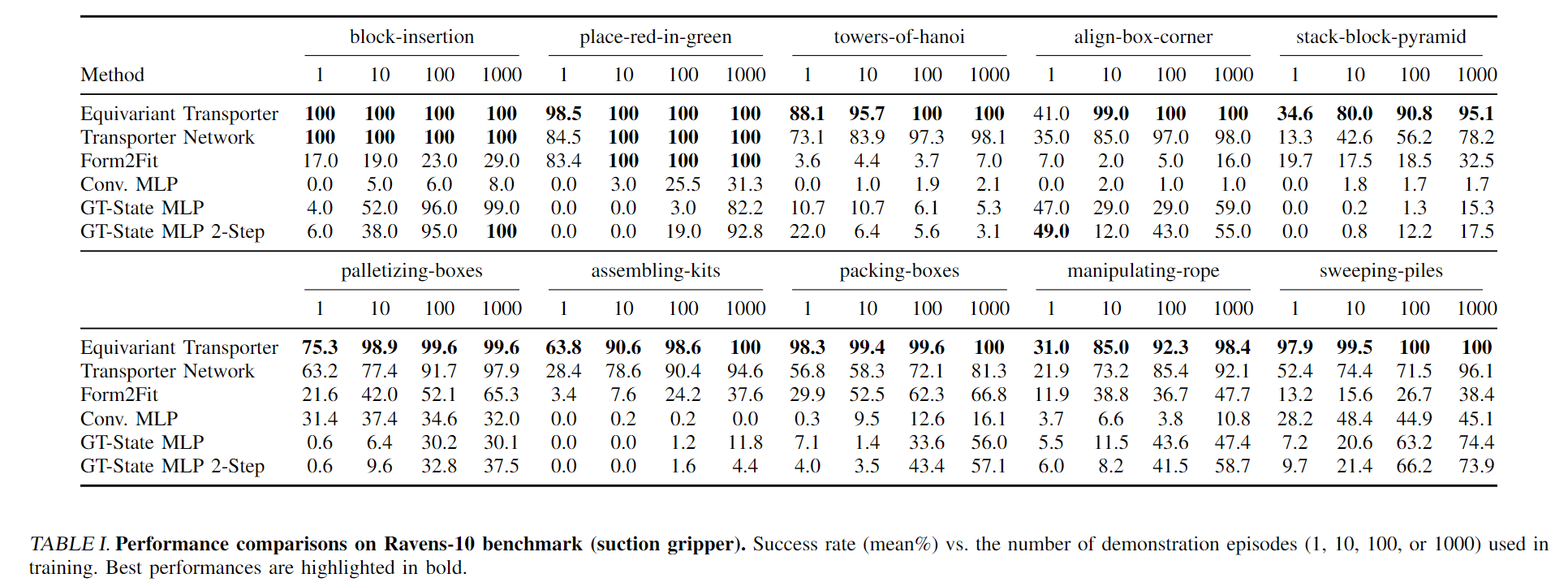
Performance Comparison

Table I shows the performance of our model on the Raven-10 tasks for different numbers of demonstrations used during training. All tests are evaluated on unseen configurations. Our proposed Equivariant Transporter Net outperforms all the other baselines in nearly all cases. The amount by which our method outperforms others is largest when the number of demonstrations is smallest, i.e. with only 1 or 10 demonstrations.

Apart from the better performance, Equivariant Transporter Network converges faster than Transporter Network. On the block insertion task, Equivariant Transporter can hit greater than 90% success rate after 10 training steps and achieve 100% succeess rate with less than 100 training steps.

Table II compares the performance of Equivariant Transporter with the baseline Transporter Net for the Parallel Jaw Gripper tasks. Again, our method outper- forms the baseline in nearly all cases.

Real Robot Experiment

Block Insertion

Place Boxes in Bowls

Stack Block Pyramid

Citation

@INPROCEEDINGS{Huang-RSS-22, 
    AUTHOR    = {Haojie Huang AND Dian Wang AND Robin Walters AND Robert Platt}, 
    TITLE     = {Equivariant Transporter Network}, 
    BOOKTITLE = {Proceedings of Robotics: Science and Systems}, 
    YEAR      = {2022}, 
    ADDRESS   = {New York City, NY, USA}, 
    MONTH     = {June}, 
    DOI       = {10.15607/RSS.2022.XVIII.007} 
} 

Contact

huang dot haoj @ northeastern dot edu